MCMC: The Gibbs Sampler, simple example w/ Matlab code

In the previous post, we compared using block-wise and component-wise implementations of the Metropolis-Hastings algorithm for sampling from a multivariate probability distribution $p(\bold x)$ . Component-wise updates for MCMC algorithms are generally more efficient for multivariate problems than blockwise updates in that we are more likely to accept a proposed sample by drawing each component/dimension independently of the others. However, samples may still be rejected, leading to excess computation that is never used. The Gibbs sampler, another popular MCMC sampling technique, provides a means of avoiding such wasted computation. Like the component-wise implementation of the Metropolis-Hastings algorithm, the Gibbs sampler also uses component-wise updates. However, unlike in the Metropolis-Hastings algorithm, all proposed samples are accepted, so there is no wasted computation.

The Gibbs sampler is applicable for certain classes of problems, based on two main criterion. Given a target distribution $p(\bold x)$ , where $\bold x = (x_1, x_2, \dots, x_D$ , ), The first criterion is 1) that it is necessary that we have an analytic (mathematical) expression for the conditional distribution of each variable in the joint distribution given all other variables in the joint. Formally, if the target distribution $p(\bold x)$ is $D$ -dimensional, we must have $D$ individual expressions for

$p(x_i|x_1,x_2,\dots,x_{i-1},x_{i+1},\dots,x_D)$

$= p(x_i | x_j), j\neq i$ .

Each of these expressions defines the probability of the $i$ -th dimension given that we have values for all other ( $j \neq i$ ) dimensions. Having the conditional distribution for each variable means that we don’t need a proposal distribution or an accept/reject criterion, like in the Metropolis-Hastings algorithm. Therefore, we can simply sample from each conditional while keeping all other variables held fixed. This leads to the second criterion 2) that we must be able to sample from each conditional distribution. This caveat is obvious if we want an implementable algorithm.

The Gibbs sampler works in much the same way as the component-wise Metropolis-Hastings algorithms except that instead drawing from a proposal distribution for each dimension, then accepting or rejecting the proposed sample, we simply draw a value for that dimension according to the variable’s corresponding conditional distribution. We also accept all values that are drawn. Similar to the component-wise Metropolis-Hastings algorithm, we step through each variable sequentially, sampling it while keeping all other variables fixed. The Gibbs sampling procedure is outlined below

set $t = 0$
generate an initial state $\bold x^{(0)} \sim \pi^{(0)}$
repeat until $t = M$

set $t = t+1$

for each dimension $i = 1..D$

draw $x_i$ from $p(x_i|x_1,x_2,\dots,x_{i-1},x_{i+1},\dots,x_D)$

To get a better understanding of the Gibbs sampler at work, let’s implement the Gibbs sampler to solve the same multivariate sampling problem addressed in the previous post.

Example: Sampling from a bivariate a Normal distribution

This example parallels the examples in the previous post where we sampled from a 2-D Normal distribution using block-wise and component-wise Metropolis-Hastings algorithms. Here, we show how to implement a Gibbs sampler to draw samples from the same target distribution. As a reminder, the target distribution $p(\bold x)$ is a Normal form with following parameterization:

$p(\bold x) = \mathcal N (\bold{\mu}, \bold \Sigma)$

with mean

$\mu = [\mu_1,\mu_2]= [0, 0]$

and covariance

$\bold \Sigma = \begin{bmatrix} 1 & \rho_{12} \\ \rho_{21} & 1\end{bmatrix} = \begin{bmatrix} 1 & 0.8 \\ 0.8 & 1\end{bmatrix}$

In order to sample from this distribution using a Gibbs sampler, we need to have in hand the conditional distributions for variables/dimensions $x_1$ and $x_2$ :

$p(x_1 | x_2^{(t-1)})$ (i.e. the conditional for the first dimension, $x_1$ )

and

$p(x_2 | x_1^{(t)})$ (the conditional for the second dimension, $x_2$ )

Where $x_2^{(t-1)}$ is the previous state of the second dimension, and $x_1^{(t)}$ is the state of the first dimension after drawing from $p(x_1 | x_2^{(t-1)})$ . The reason for the discrepancy between updating $x_1$ and $x_2$ using states $(t-1)$ and $(t)$ , can be is seen in step 3 of the algorithm outlined in the previous section. At iteration $t$ we first sample a new state for variable $x_1$ conditioned on the most recent state of variable $x_2$ , which is from iteration $(t-1)$ . We then sample a new state for the variable $x_2$ conditioned on the most recent state of variable $x_1$ , which is now from the current iteration, $t$ .

After some math (which which I will skip for some brevity, but see the following for some details), we find that the two conditional distributions for the target Normal distribution are:

$p(x_1 | x_2^{(t-1)}) = \mathcal N(\mu_1 + \rho_{21}(x_2^{(t-1)} - \mu_2),\sqrt{1-\rho_{21}^2})$

and

$p(x_2 | x_1^{(t)})=\mathcal N(\mu_2 + \rho_{12}(x_1^{(t)}-\mu_1),\sqrt{1-\rho_{12}^2})$ ,

which are both univariate Normal distributions, each with a mean that is dependent on the value of the most recent state of the conditioning variable, and a variance that is dependent on the target covariances between the two variables.

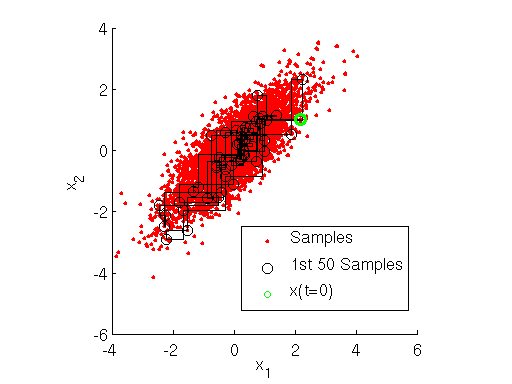
Using the above expressions for the conditional probabilities of variables $x_1$ and $x_2$ , we implement the Gibbs sampler using MATLAB below. The output of the sampler is shown here:

Inspecting the figure above, note how at each iteration the Markov chain for the Gibbs sampler first takes a step only along the $x_1$ direction, then only along the $x_2$ direction. This shows how the Gibbs sampler sequentially samples the value of each variable separately, in a component-wise fashion.

% EXAMPLE: GIBBS SAMPLER FOR BIVARIATE NORMAL
rand('seed' ,12345);
nSamples = 5000;
 
mu = [0 0]; % TARGET MEAN
rho(1) = 0.8; % rho_21
rho(2) = 0.8; % rho_12
 
% INITIALIZE THE GIBBS SAMPLER
propSigma = 1; % PROPOSAL VARIANCE
minn = [-3 -3];
maxx = [3 3];
 
% INITIALIZE SAMPLES
x = zeros(nSamples,2);
x(1,1) = unifrnd(minn(1), maxx(1));
x(1,2) = unifrnd(minn(2), maxx(2));
 
dims = 1:2; % INDEX INTO EACH DIMENSION
 
% RUN GIBBS SAMPLER
t = 1;
while t < nSamples
    t = t + 1;
    T = [t-1,t];
    for iD = 1:2 % LOOP OVER DIMENSIONS
        % UPDATE SAMPLES
        nIx = dims~=iD; % *NOT* THE CURRENT DIMENSION
        % CONDITIONAL MEAN
        muCond = mu(iD) + rho(iD)*(x(T(iD),nIx)-mu(nIx));
        % CONDITIONAL VARIANCE
        varCond = sqrt(1-rho(iD)^2);
        % DRAW FROM CONDITIONAL
        x(t,iD) = normrnd(muCond,varCond);
    end
end
 
% DISPLAY SAMPLING DYNAMICS
figure;
h1 = scatter(x(:,1),x(:,2),'r.');
 
% CONDITIONAL STEPS/SAMPLES
hold on;
for t = 1:50
    plot([x(t,1),x(t+1,1)],[x(t,2),x(t,2)],'k-');
    plot([x(t+1,1),x(t+1,1)],[x(t,2),x(t+1,2)],'k-');
    h2 = plot(x(t+1,1),x(t+1,2),'ko');
end
 
h3 = scatter(x(1,1),x(1,2),'go','Linewidth',3);
legend([h1,h2,h3],{'Samples','1st 50 Samples','x(t=0)'},'Location','Northwest')
hold off;
xlabel('x_1');
ylabel('x_2');
axis square

Wrapping Up

The Gibbs sampler is a popular MCMC method for sampling from complex, multivariate probability distributions. However, the Gibbs sampler cannot be used for general sampling problems. For many target distributions, it may difficult or impossible to obtain a closed-form expression for all the needed conditional distributions. In other scenarios, analytic expressions may exist for all conditionals but it may be difficult to sample from any or all of the conditional distributions (in these scenarios it is common to use univariate sampling methods such as rejection sampling and (surprise!) Metropolis-type MCMC techniques to approximate samples from each conditional). Gibbs samplers are very popular for Bayesian methods where models are often devised in such a way that conditional expressions for all model variables are easily obtained and take well-known forms that can be sampled from efficiently.

Gibbs sampling, like many MCMC techniques suffer from what is often called “slow mixing.” Slow mixing occurs when the underlying Markov chain takes a long time to sufficiently explore the values of $\bold x$ in order to give a good characterization of $p(\bold x)$ . Slow mixing is due to a number of factors including the “random walk” nature of the Markov chain, as well as the tendency of the Markov chain to get “stuck,” only sampling a single region of $\bold x$ having high-probability under $p(\bold x)$ . Such behaviors are bad for sampling distributions with multiple modes or heavy tails. More advanced techniques, such as Hybrid Monte Carlo have been developed to incorporate additional dynamics that increase the efficiency of the Markov chain path. We will discuss Hybrid Monte Carlo in a future post.

Victor Fang

Blogs on AI, machine learning, blockchain, startup and life in San Francisco

MCMC: The Gibbs Sampler, simple example w/ Matlab code

http://theclevermachine.wordpress.com/tag/gibbs-sampler/